Filtro FIR con pipeline

Filtro FIR con pipeline

I circuiti digitali tendono sempre di più a sostituire i circuiti analogici in parecchi campi. I segnali analogici possono essere infatti trasformati, mediante dispositivi detti convertitori analogico-digitale (analog-to-digital converters, ADC) in una serie di numeri binari che ne rappresentano la codifica. Questi numeri binari possono quindi essere elaborati da circuiti digitali veloci con estrema precisione, e poi essere ritrasformati in forma analogica mediante dei convertitori digitale-analogico, (digital-to-analog converters, DAC). I vantaggi delle rappresentazioni numeriche di segnali analogici sono molteplici: diventa possibile eseguire trattamenti del segnale anche fuori linea e su normali calcolatori general-purpose, è possibile conseguire una grandissima precisione, accuratezza e ripetibilità delle elaborazioni senza la necessità di ricorrere a componenti eccessivamente costosi, e così via.

Supponiamo allora di voler realizzare un filtro digitale a risposta impulsiva finita (finite impulse response, FIR) che realizzi un prodotto di convoluzione discreta secondo la seguente formula:

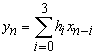
dove y_n sono i valori dei campioni che il circuito deve fornire in uscita, h_i sono delle costanti numeriche date e x_i sono dei campioni digitali di un segnale analogico. I dati x_n arrivano in ingresso con una frequenza di 10 Mhz (ossia uno ogni 100 nsec), organizzati in pacchetti da 1024 campioni. Ad ogni nuovo campione il circuito deve calcolare la sommatoria utilizzando quel campione ed i tre precedenti, emettendo in uscita il corrispondente risultato y_n. I sommatori e i moltiplicatori a disposizione hanno ritardi massimi di propagazione rispettivamente di 30 e di 60 nsec: la somma di questi tempi è quindi leggermente inferiore all’intervallo di tempo tra due campioni consecutivi.

I dati x_n in ingresso sono formati da 8 bit in virgola fissa in cui il bit più significativo rappresenta la parte intera ed è sempre nullo, ed i 7 bit rimanenti rappresentano la parte frazionaria del dato. Si ha quindi che . La stessa cosa vale per gli h_i. I dati in uscita devono essere ancora ad 8 bit, ma non viene specificato alcun particolare formato per quanto riguarda la posizione del punto frazionario. Dovremo quindi adottare opportuni accorgimenti per mantenere in uscita il maggior numero possibile di bit significativi.

E' ovvio che il concetto di punto frazionario è esclusivamente basato sull’interpretazione che si attribuisce ad una determinata rappresentazione numerica. I circuiti aritmetici per l’esecuzione della somma e della moltiplicazione non hanno modo di sapere se i loro operandi sono numeri interi ovvero reali in virgola fissa, ma utilizzano sempre lo stesso algoritmo a prescindere dal fatto che gli operandi siano interi o meno. Sta all'utilizzatore di questi circuiti fissare la posizione "virtuale" del punto frazionario all’interno degli operandi e quindi interpretare in maniera corretta i risultati prodotti. In particolare, occorre prestare attenzione al fatto che i due addendi in ingresso ai sommatori devono avere uno stesso numero di bit per la parte intera, in modo che il punto frazionario sia correttamente allineato.

Un circuito moltiplicatore esegue semplicemente il prodotto tra due numeri interi assoluti ad 8 bit e ne emette uno a 16 bit. Se, nel nostro caso, i due numeri che si vanno a moltiplicare hanno un bit intero e 7 frazionari (hanno cioè formato 1.7), allora il risultato della moltiplicazione avrà due bit interi e 14 frazionari (ossia formato 2.14). Dal momento che entrambi i fattori hanno per ipotesi parte intera nulla, anche il prodotto avrà la parte intera, ossia i due bit più significativi, nulla. Il formato del risultato delle moltiplicazioni sarà quindi:

00.b₁b₂b₃b₄b₅b₆b₇b₈b₉b₁₀b₁₁b₁₂b₁₃b₁₄

Un circuito sommatore esegue la somma tra due interi a 16 bit e produce un intero ancora a 16 bit. È chiaro che, se i due operandi hanno il punto frazionario nella stessa posizione, anche il risultato avrà il punto frazionario nella medesima posizione. Poiché i quattro numeri che dobbiamo sommare sono tutti minori di 1, il risultato della sommatoria sarà sicuramente compreso tra 0 e 4 (escluso). Per inviare in uscita 8 bit mantenendo il massimo numero possibile di bit frazionari, basterà quindi rappresentare il risultato in formato 2.6 ed emettere gli 8 bit più significativi dell’uscita dai sommatori in modo che i due bit più significativi rappresentino la parte intera ed i rimanenti 6 quella frazionaria.

Passiamo ora alla progettazione del circuito. Per prima cosa supponiamo di disporre di un segnale di clock (CLK) proveniente dall'esterno che, in corrispondenza di ogni fronte di salita, indichi l'arrivo di un nuovo dato in ingresso sulle 8 linee dati di x_n. I coefficienti h_i sono delle costanti numeriche, che possiamo supporre memorizzate in quattro registri separati. Per eseguire i calcoli richiesti, tuttavia, dobbiamo disporre, oltre che del campione corrente x_n, anche dei tre campioni precedenti x_n-1, x_n-2, x_n-3 ; il modo più semplice è utilizzare una cascata (pipeline) di registri ad 8 bit, come illustrato in Fig. 1. Ad ogni fronte attivo del clock ciascun registro memorizza il contenuto del registro che lo precede (oppure, nel caso del primo registro del pipeline, le linee x_n), eseguendo quindi uno shift verso destra delle informazioni.

A questo punto si possono connettere i circuiti che eseguono la moltiplicazione e quelli che eseguono l'addizione. Poiché si hanno a disposizione solo addizionatori con due operandi, la somma di quattro numeri deve essere realizzata con un "albero" di addizionatori, come appare in Fig. 2, dove con le lettere greche P e S abbiamo contrassegnato rispettivamente il moltiplicatore e l'addizionatore.

Questa soluzione presenta tuttavia un grave inconveniente. I dati arrivano in ingresso ogni 100 nsec, mentre il ritardo complessivo di propagazione attraverso i livelli di moltiplicazione e di addizione è pari a 30 + 30 + 60 = 120 nsec, il che significa che con l’organizzazione di Fig. 2 non riusciamo a produrre risultati con la stessa velocità dei dati in ingresso. La soluzione consiste nell’introdurre uno stadio di pipeline tra i due livelli di sommatori, come appare in Fig. 3.

In tal modo, il ritardo di propagazione della porzione di circuito a monte dello stadio di pipeline introdotto è di circa 90 nsec, a cui si va ad aggiungere il ritardo introdotto dai registri di pipeline che in genere è di qualche nanosecondo, per un totale di di circa 93-95 nsec. Il ritardo di propagazione della porzione di circuito a valle del pipeline è di 30 nsec, per cui rimane un margine di circa 70 nsec in cui il risultato in uscita rimane sicuramente stabile. Se il ritardo limite di 93-95 nsec può sembrare critico perché troppo vicino ai 100 nsec di intervallo tra un dato e l'altro, sarà sufficiente posizionare i registri di pipeline tra il livello dei moltiplicatori e quello degli addizionatori: in questo caso l’intero circuito viene partizionato in in due sottocircuiti ciascuno con ritardo di propagazione di circa 60 nsec, ma il pipeline richiede 4 registri a 16 bit invece di 2.

Non sempre, tuttavia, le soluzioni semplici sono le migliori. Esiste infatti un’organizzazione diversa da quella presentata sinora, che ha non solo il vantaggio di presentare meno problemi legati ai ritardi di propagazione nei vari moduli, ma soprattutto è facilmente espandibile qualora la sommatoria dovesse essere estesa ad un numero maggiore di addendi (la soluzione vista finora, invece, comporterebbe la riprogrttazione dell’intero albero dei sommatori ed eventualmente il riposizionamento degli stadi di pipeline).

L’osservazione che ci conduce ad una organizzazione dei circuiti radicalmente diversa è che la formula originale può essere sviluppata in una forma più favorevole all’implementazione. Anziché calcolare in parallelo i prodotti h₀x₀, h₁x_n-1, h₂x_n-2, h₃x_n-3, tra ciascuno dei coefficienti ed un dato variabile, supponiamo di calcolare in parallelo i prodotti:

Seguendo questa notazione, è facile verificare che il valore di uscita può alternativamente essere calcolato come:

Questa espressione conduce direttamente all’implementazione illustrata in Fig. 4. Si noti che i cofficienti h_i vengono moltiplicati in ordine inverso rispetto al circuito precedente.

(Il registro sugli ingressi x_n ha la funzione di sincronizzare i dati di ingresso e renderli stabili per un intero periodo di clock.) Questa organizzazione comporta molteplici vantaggi. I quattro registri a 16 bit servono al duplice scopo di "ritardare nel tempo'', per così dire, le quattro moltiplicazioni che vengono eseguite in parallelo, e di operare come registri di pipeline. A valle di ogni registro, infatti, si sommano i ritardi di propagazione di un sommatore e di un moltiplicatore, per un totale di 90 nsec. Sono stati eliminati non solo i 3 registri ad 8 bit che prima erano necesssari per memorizzare x_n-1, x_n-2, ed x_n-3, ma anche tutti i registri di pipeline utilizzati per partizionare il blocco moltiplicatori-addizionatori; al loro posto, vengono utilizzati solamente tre registri a 16 bit. (Sull'uscita y_n è stato previsto un ulteriore registro per portare a quasi 100 nsec l’intervallo di stabilità del risultato.) Quel che va messo in evidenza, tuttavia, è che il circuito può essere esteso ad un numero qualunque di addendi semplicemente aggiungendo un ulteriore moltiplicatore, un sommatore ed un registro per ogni nuovo addendo della sommatoria.

Se tutti i registri del circuito vengono azzerati in assenza di dati all’ingresso, i primi tre valori della sequenza delle uscite y_n saranno i seguenti:

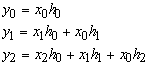
e dal quarto in poi assumeranno i corretti valori dati dalla sommatoria. Si noti che, avendo inserito un ulteriore registro di pipeline sull'uscita, ogni risultato y_n appare con un clock di ritardo rispetto al corrispondente x_n (Fig. 5).

Filtro FIR con pipeline

© 1997-2003 Paolo Marincola (Rome, Italy)
e-mail: pmaNOSPAM@acm.org (eliminare i caratteri "NOSPAM" per ottenere l'indirizzo esatto)
Commenti, osservazioni e suggerimenti sono estremamente graditi.

Last revised: 2003-12-06 19:51