Reti neurali e riconoscimento di caratteri |
|
Il cervello umano è unanimemente considerato, se non il più complesso, certamente uno dei più complessi sistemi conosciuti in natura, sia sotto l'aspetto della struttura anatomica che sotto quello delle capacità cognitive e dei meccanismi funzionali, ancora in gran parte ignoti. Come apparato per il trattamento di informazioni, esso racchiude in una massa di circa 1.5 kg una macchina indiscutibilmente di gran lunga più potente1 di qualunque calcolatore finora costruito dall'uomo, sebbene i suoi elementi costitutivi abbiano velocità di elaborazione inferiori di diversi ordini di grandezza a quella delle unità centrali degli odierni calcolatori.
Allo stesso tempo, non vi è ormai più alcun dubbio che la straordinaria efficienza del cervello nello svolgimento sia di funzioni inferiori (comuni cioè anche ad altri animali, come la visione, l'udito, e così via) sia di funzioni superiori apparentemente tipiche solo dell'uomo, come la formazione di concetti o la capacità di pianificazione, debba essere essenzialmente ascritta al numero enorme di cellule nervose -- 1012, secondo recenti stime (Kandel & Schwartz, 1985), ma è possibile che siano molte di più -- che lo costituiscono, ed al numero ancora più grande (per un fattore di 103-104) di interconnessioni che esse formano tra di loro. La possibilità di modellare il funzionamento della singola cellula nervosa, o neurone, e della singola interconnessione, o sinapse, secondo uno schema relativamente semplice (come avremo modo di vedere più avanti) conduce peraltro alla conclusione che il cervello sia in grado di risolvere una vastissima classe di problemi anche estremamente complessi mediante la loro suddivisione in un numero sufficientemente grande di sottoproblemi elementari e l'elaborazione in forma massivamente parallela di una grandissima quantità di informazioni.
La ricerca neurofisiologica sulla struttura funzionale e sui meccanismi di elaborazione del cervello e del sistema nervoso in generale, iniziata fin dagli albori della medicina, è avanzata con fatica, sia per ragioni tecnologiche dovute all'inadeguatezza -- e talora alla totale mancanza -- delle metodologie e della strumentazione di indagine, sia per ragioni culturali legate ad una apparente estraneità della visione sistemistica nella pratica e nella teoria medica; il bagaglio di conoscenze è diventato tuttavia ricchissimo e in continua espansione, tanto che al giorno d'oggi alcune aree del sistema nervoso possono dirsi sufficientemente ben conosciute, sia dal punto di vista anatomico che dal punto di vista funzionale.
Col progredire delle scienze informatiche, tuttavia, si è venuta affermando un'ulteriore motivazione allo studio approfondito del sistema nervoso in generale e del cervello in particolare, ed è quella che punta alla cosiddetta intelligenza artificiale, il cui obiettivo dichiarato è la costruzione di apparati di elaborazione capaci di comportamenti che possano essere definiti intelligenti.
L'idea di costruire sistemi di elaborazione che imitassero il funzionamento del cervello umano è molto meno recente di quanto si possa credere, e il primo cenno scritto può esser fatto risalire addirittura all'Iliade, dove si racconta degli automi costruiti da Efesto, dio del fuoco. Anche limitandoci ad epoche molto recenti, basterà ricordare come lo stesso von Neumann, benché talvolta scettico a riguardo delle connessioni tra cervello e calcolatore (von Neumann, 1951, 1958), quando nel 1945 fu incaricato di stendere le specifiche per un calcolatore elettronico più potente dell'ENIAC, rimase a lungo indeciso (McCorduck, 1979) se ricorrere a una struttura fortemente parallela, analoga a quella del sistema nervoso, oppure a quell'architettura sequenziale a programma memorizzato che ancor oggi porta il suo nome; e optò alla fine per la seconda alternativa soltanto per via delle limitazioni tecnologiche del tempo, che non gli avrebbero consentito di realizzare una macchina parallela di prestazioni adeguate (von Neumann, 1982).
Le scarse cognizioni che ancora negli anni '40 si avevano a disposizione sulla struttura e sulla funzionalità del sistema nervoso non impedirono a W. S. McCulloch, un neurofisiologo, e a W. Pitts, un giovane matematico, di proporre un modello estremamente semplice di cellula nervosa, e di dimostrarne in maniera rigorosa le capacità computazionali (McCulloch & Pitts, 1943; Pitts & McCulloch, 1947; McCulloch, 1965). In seguito F. Rosenblatt (1958, 1961) estese e sofisticò il modello di McCulloch-Pitts fino al punto di costruire reti neurali costituite da cellule artificiali, chiamate perceptron, in grado sia di classificare pattern sia addirittura di apprendere dall'esperienza (Rosenblatt, 1959). Circa nello stesso periodo B. Widrow e M. E. Hoff2 proposero un "neurone adattativo" con cui costruire delle reti di controllo in grado di adattarsi alle variazioni ambientali (Widrow & Hoff, 1960). Fu soltanto verso la fine degli anni '60, quando l'entusiasmo prodotto da queste ricerche era diventato ormai enorme (e certamente anche spropositato), tanto da considerare la costruzione di "macchine intelligenti" solo come un banale problema tecnologico, che Minsky e Papert (1969) dimostrarono l'incapacità del perceptron di risolvere determinati problemi di classificazione, peraltro molto semplici come impostazione. Da quel momento in poi, la ricerca su questi modelli e sulle loro applicazioni cessò immediatamente, mentre tutti gli sforzi venivano concentrati sull'Intelligenza Artificiale classica, basata sull'elaborazione di simboli anziché sull'elaborazione distribuita (Minsky, 1963; Feigenbaum & Feldman, 1963), della quale lo stesso Minsky era già uno dei principali esponenti fin dallo storico convegno di Dartmouth del 1956 in cui ne erano state gettate le basi.
La ricerca sulle reti neurali in realtà proseguiva, sostenuta solo dall'ostinazione di ricercatori isolati, provenienti per lo più dal campo neurofisiologico, spesso privi di fondi e costretti a pubblicare i resoconti del loro lavoro su periodici in gran parte sconosciuti alla comunità scientifica. Tuttavia, mentre nel periodo d'oro precedente la gran parte delle ricerche era orientata verso la costruzione di calcolatori neurali, la ricerca di questo periodo, mirabilmente esemplificata dall'enorme quanto oscuro lavoro svolto da S. Grossberg (1982, 1987), venne piuttosto rivolta alla modellazione delle reti con lo scopo di fornire giustificazioni a certi comportamenti ben noti agli psicologi (come i riflessi condizionati alla Pavlov, o certe illusioni ottiche) ma rimasti assolutamente inspiegati a livello neurofisiologico.
Il seguito della storia assume per molti versi aspetti abbastanza ironici. Gli stessi Minsky e Papert, nel loro lavoro critico, avevano individuato nella struttura ancora troppo semplice delle reti costituite da perceptron la causa della loro incapacità ad essere addestrate ad affrontare certe classi di problemi, e avevano mostrato come strutture più complesse, dette perceptron multilivello (multilevel perceptron) potessero superare, almeno in linea teorica, tali limitazioni; ma ad esse, purtroppo, non potevano essere applicate le procedure di addestramento allora note. L'algoritmo necessario fu poi scoperto da Werbos (1974) pochi anni dopo, ma, pur essendo stato pubblicato in una tesi di dottorato di cui lo stesso Grossberg era relatore, rimase del tutto sconosciuto; venne ancora riscoperto da Parker (1982), ma anche in questo caso la comunità scientifica ne rimase totalmente all'oscuro. Fu proprio in questo periodo, a dire il vero, che si ebbe un primo risveglio di interesse nelle reti neurali per merito di due lavori di Hopfield (1982, 1984), un fisico rinomato e autorevole, che non solo per la prima volta riuscì a quantificare le capacità computazionali dei neuroni formali, ma fu soprattutto capace, nel corso di diverse conferenze tenute in tutto il mondo, di convincere centinaia di ricercatori a superare pregiudizi ormai radicati e a riavvicinarsi alle reti neurali. Fu però solo a metà degli anni '80, quando la procedura di addestramento del perceptron multilivello venne riscoperta per la terza volta (Rumelhart et al., 1986) sotto il nome di back-propagation, che la notizia si diffuse in maniera estremamente rapida, provocando in brevissimo tempo una vera e propria esplosione delle ricerche nel campo delle reti neurali.3 Sostenute da una conoscenza del sistema nervoso significativamente più profonda che non quella della metà del secolo, ma mitigate anche dalla consapevolezza dei precedenti fallimenti, sono oggi risorte le speranze (e, in un certo senso, anche le illusioni) relative alla possibilità di costruire macchine intelligenti, proprio mentre diventa sempre più evidente come l'intelligenza artificiale "classica", nonostante la potenza spropositata dei calcolatori ad essa dedicati e il conseguimento di alcuni risultati certamente pregevoli, come i cosiddetti sistemi esperti, abbia sostanzialmente fallito pressoché tutti i propri ambiziosi obiettivi iniziali e si dibatta in una strada senza uscita -- come recentemente anche lo stesso Minsky (1985) sembra ormai ammettere.
Come vedremo meglio più avanti, i due approcci all'intelligenza artificiale non potrebbero essere più diversi, anche se non sono mancati i tentativi di farli in qualche modo coesistere. L'approccio "classico" è basato sull'elaborazione puramente sequenziale di entità simboliche: come in una macchina di Turing, nessun problema può essere risolto se non si conosce un algoritmo che ne determini la soluzione, se cioè non è disponibile una procedura rigorosamente definita che dai dati di ingresso produca i dati di uscita, e che quindi possa essere implementata su un calcolatore a programma memorizzato come quelli che oggi conosciamo. L'approccio neurale, o più precisamente connessionista, invece, è basato su una rete di elementi computazionali (cellule) dalle capacità elementari ma fittamente interconnessi, dove il comportamento "intelligente" è una proprietà emergente dal complesso delle interazioni tra le varie cellule; i dati immessi, elaborati o prodotti non sono simboli, ma pattern di attività degli elementi computazionali; non esistono algoritmi specifici per la soluzione di classi specifiche di problemi, ma esistono soltanto procedure standardizzate di addestramento che consentono alla rete di apprendere dall'esperienza e di autoconfigurarsi nella maniera più appropriata in funzione dei problemi specifici. Questo concetto, che rientra nei limiti della normalità quando riferito ai sistemi biologici, diventa ricchissimo di implicazioni, addirittura rivoluzionario, se applicato all'elaborazione dei dati mediante macchine artificiali.
Le indagini neuroanatomiche hanno scoperto una varietà enorme di neuroni, con differenze fondamentali nella struttura morfologica, negli schemi di interconnessione e nei meccanismi di ricezione e trasmissione dei segnali nervosi, senza che sia ancora chiaro quale ruolo possano avere tali differenze in una descrizione puramente funzionale dei meccanismi cerebrali. Per di più, la conoscenza attuale sia del funzionamento del singolo neurone che delle interazioni tra neuroni è per molti versi limitata, e non mancano aspetti ancora virtualmente sconosciuti. Tuttavia, vi sono delle proprietà e dei meccanismi comuni a pressoché tutti i neuroni, ed è di questi aspetti che daremo qui un brevissimo cenno.
Il neurone (Fig. 16) è una cellula altamente specializzata,finora ritenuta incapace di autoriprodursi, costituita essenzialmente da quattro parti principali: un corpo cellulare o soma, delle arborizzazioni dette dendriti, un prolungamento per la trasmissione dei segnali nervosi detto assone, la cui parte finale si ramifica in un numero più o meno grande di collaterali. Il soma contiene il nucleo cellulare e un gran numero di strutture che sovrintendono ai processi vitali della cellula; la sua forma varia considerevolmente a seconda del tipo di neurone. I dendriti hanno come funzione principale quella di ricevere i messaggi nervosi provenienti da altri neuroni, di combinarli e di trasmetterli, attraverso la membrana cellulare, verso la parte centrale della cellula. Il segnale nervoso, di natura elettrochimica, ha origine dal punto in cui l'assone fuoriesce dal soma e, mediante complessi meccanismi di scambio ionico ormai in gran parte noti, si propaga attraverso l'assone (che può essere lungo anche fino a 1 metro nell'Uomo) fino ai collaterali, con velocità che possono raggiungere anche i 100 metri al secondo.
|
L'estremità finale del collaterale termina in una struttura detta bottone sinaptico (Fig. 17) che forma una giunzione solitamente con un dendrite (sinapsi asso-dendritica), ma si conoscono casi di giunzioni formate con la membrana del soma di un neurone (sinapsi asso-somatiche), con la superficie di un assone (sinapsi asso-assoniche), o addirittura con un altro bottone sinaptico (sinapsi asso-sinaptiche); sono ancora possibili giunzioni con vasi capillari o con fibre muscolari; sono infine noti casi di collaterali che terminano con una sinapsi nel liquido extracellulare, ma la funzione di tali strutture è del tutto sconosciuta. Il bottone sinaptico è in realtà separato dalla superficie del dendrite da uno spazio intersinaptico riempito di fluido extracellulare;4 all'arrivo dell'impulso nervoso, dall'interno del bottone sinaptico vengono emessi pacchetti di sostanze chimiche dette neurotrasmettitori, che superano lo spazio intersinaptico e vengono assorbite attraverso la membrana post-sinaptica.
|
La presenza e la distribuzione di vari tipi di ioni (sodio, potassio e diversi altri) sia all'interno che all'esterno del corpo cellulare, come pure la permeabilità selettiva della membrana cellulare alle varie specie ioniche, fanno sì che in condizioni di riposo l'interno del neurone si trovi ad un potenziale di circa -70 mV rispetto all'esterno (potenziale di membrana a riposo). La stimolazione di tale potenziale verso valori più positivi (depolarizzazione), che può essere provocata sia artificialmente sia mediante opportuna concentrazione di determinati tipi di neurotrasmettitori, quando supera i -65 mV, dà luogo (Fig. 18) ad un aumento improvviso del potenziale fino a valori di circa +40 mV e ad un successivo immediato abbassamento fino a circa -80 mV (iperpolarizzazione), seguito poi da un lento ritorno al valore di riposo; questo fenomeno di rapidissima inversione del potenziale di membrana, della durata approssimativa di 2-3 msec, è detto potenziale d'azione, e una volta generato si propaga lungo tutto l'assone, sotto forma di impulso nervoso. Raramente l'impulso nervoso è isolato, anzi in generale l'informazione trasmessa è strutturata in treni periodici di impulsi, la cui massima frequenza è tuttavia limitata dalla durata del periodo di iperpolarizzazione, entro il quale non può mai insorgere un nuovo potenziale d'azione.
|
Ogni giunzione sinaptica è caratterizzata dal tipo di neurotrasmettitore che essa è in grado di liberare: vi sono sostanze neurotrasmettitrici, come l'acetilcolina, in grado di favorire la scarica del neurone, mentre altre, come la dopamina o l'acido gamma-amminobutirrico, la rendono più difficoltosa; le corrispondenti giunzioni sinaptiche vengono allora dette rispettivamente eccitatorie e inibitorie.
Le reti costituite dall'interconnessione dei neuroni (dette talvolta reti neuronali, per distinguerle da quelle formate da neuroni artificiali) sono estremamente complesse. Ciascun neurone può formare sinapsi con un gran numero di altri neuroni, da 1 000 a 10 000 in genere; certi tipi di neuroni del cervelletto (cellule di Purkinje) arrivano a formare fino a 150 000 sinapsi con cellule analoghe (Kandel & Schwartz, 1985). Un esempio molto significativo della complessità delle reti nervose e del numero di elementi che le costituiscono è dato senza dubbio dal sistema visivo dell'Uomo: la retina è costituita da circa 125 milioni di cellule nervose specializzate, i fotorecettori, in grado di convertire la luce in segnali nervosi; questi segnali vengono pre-elaborati localmente mediante 5 strati di neuroni ed inviati attraverso il nervo ottico, costituito da circa 1 milione di fibre assoniche, ad una struttura detta nucleo genicolato laterale costituita da 6 strati di neuroni, la quale a sua volta riceve ed emette segnali da e verso la corteccia visiva primaria, disposta nel lobo occipitale dell'encefalo (Hubel, 1988); da qui, si dipartono grossi fasci nervosi verso le aree corticali preposte ai processi mentali superiori, ancora praticamente inesplorate.
Il neurone artificiale viene nella gran parte dei casi progettato in modo da imitare le caratteristiche del neurone biologico. Va tuttavia sottolineato come questa rassomiglianza sia estremamente approssimativa, poiché il comportamento del neurone biologico è di gran lunga più complesso di qualunque neurone artificiale finora utilizzato,5 e non tutti i suoi aspetti possono ancora dirsi del tutto chiariti.
In quasi tutti i neuroni artificiali si assume che i segnali x1, x2, ..., xN ad essi applicati come ingressi vengano combinati linearmente mediante una serie di pesi w1, w2, ..., wN che rappresentano l'efficienza delle connessioni attraverso cui i segnali vengono trasportati; pesi positivi rappresentano connessioni eccitatorie, mentre pesi negativi rappresentano connessioni inibitorie. Il risultato della combinazione lineare è dunque l'eccitazione netta u applicata al neurone:
u = x1 w1 + x2 w2 + ... + xN wN
Se rappresentiamo mediante vettori a N componenti sia gli ingressi:
x = [x1 x2 ... xN]T
(dove l'esponente T indica trasposizione) sia i pesi:
w = [w1 w2 ... wN]T
allora l'eccitazione netta è semplicemente il prodotto scalare tra il vettore degli ingressi e il vettore dei pesi:
u = wT x
Di solito, tuttavia, l'eccitazione netta non costituisce l'uscita del neurone, ma viene modulata mediante una funzione non lineare f(u), detta funzione di attivazione, che genera il segnale di uscita o attività y:
y = f(u)
Le funzioni di attivazione prevalentemente usate sono:
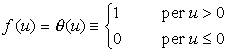
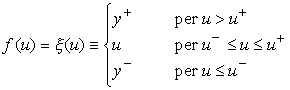
dove u+, u-, y+, y- sono costanti reali, con u- < u+, y- < y+;
![]()
f(u) = tanh u
Il neurone può infine essere dotato di una soglia interna b, detta bias, in modo tale che la sua attività viene calcolata come
y = f(u - b)
Tuttavia, sebbene abbia un qualche corrispettivo biologico, tale soglia rappresenta soltanto un'inutile complicazione formale, poiché essa può sempre essere trasformata in un'ulteriore connessione entrante di peso –b cui è applicato un ingresso di valore sempre uguale ad 1; pertanto, nel seguito non terremo più conto di essa.
Modelli così semplici, come abbiamo già accennato, ignorano molte caratteristiche del neurone biologico; ad esempio, non vengono presi in considerazione i ritardi di propagazione, che possono avere conseguenze importantissime sulla dinamica del sistema, né vengono sfruttati gli effetti dovuti alla modulazione in frequenza dei segnali biologici, che molti ricercatori considerano invece essenziali. Nonostante queste limitazioni, le reti che vengono costruite con neuroni così modellati hanno architetture analoghe a quelle trovate nei sistemi nervosi animali: soltanto ulteriori ricerche potranno stabilire se semplificazioni così grossolane possono ancora tornare di qualche utilità.
Sebbene il singolo neurone formale sia già in grado di portare a termine con successo alcuni semplici processi di pattern recognition, le potenzialità di questo approccio possono essere apprezzate solo passando a configurazioni di più neuroni. La rete più semplice è costituita da un gruppo di neuroni disposti in uno strato (layer), come illustrato in Fig. 23a, dove ciascuno degli N segnali di ingresso è connesso a ciascuno di M neuroni mediante una connessione dotata di un proprio peso. L'insieme dei pesi costituisce adesso una matrice W ad M righe ed N colonne, il cui generico elemento wij è il peso della connessione tra l'ingresso xj e l'i-esimo neurone; in tal modo l'uscita della rete può essere descritta mediante un vettore:
y = [y1 y2 ... yM]T = f(Wx)
|
È possibile costruire reti ancora più complesse, dette multilayer, disponendo più strati di neuroni in cascata (Fig. 23b,c), nelle quali appare finalmente evidente il ruolo delle non-linearità nelle funzioni di attivazione. Siano infatti W1, W2, ..., Wk le matrici dei pesi di ciascuno strato di una rete a k strati; se le funzioni di attivazione fossero lineari, se cioè l'uscita di ogni neurone fosse semplicemente proporzionale per un fattore H alla sua eccitazione netta, allora l'uscita della rete verrebbe ad essere:
y = Hk W1 W2 ... Wk = Hk W
dove W è il prodotto delle matrici W1, W2, ..., Wk. Il comportamento della rete a k strati sarebbe in tal caso equivalente a quello di una rete a un solo strato con matrice dei pesi W e costante di proporzionalità Hk tra eccitazione e attivazione. E' chiaro che un'equivalenza del genere non può essere stabilita se la funzione di attivazione presenta delle non-linearità.
Tutte le reti cui fin qui abbiamo accennato sono del tipo feed-forward, in cui cioè le connessioni uscenti da ogni neurone raggiungono soltanto neuroni appartenenti a strati superiori. Se invece si ammettono connessioni tra neuroni dello stesso strato, oppure connessioni verso neuroni di strati inferiori, si ottiene un'ulteriore classe di reti neurali, quella delle reti feed-back (dette anche ricorrenti). E' facile comprendere come vi sia una profonda differenza di comportamento tra le reti feed-forward e le reti ricorrenti: mentre l'uscita delle prime può essere calcolata subito dopo l'applicazione dell'ingresso, le seconde presentano in genere un'evoluzione che passa attraverso una sequenza di stati della rete, e che in certi casi può anche portare all'instabilità della rete stessa. Sotto l'aspetto formale, dunque, una rete neurale può essere definita in termini estremamente generali come un sistema dinamico con la topologia di un grafo orientato, in grado di elaborare informazioni attraverso la sua risposta ad un ingresso continuo o momentaneo (Hecht-Nielsen, 1987). La dinamica delle reti ricorrenti si ricollega per certi versi a quella dei sistemi non-lineari, ed è pertanto soggetta a diverse complicazioni teoriche, che tuttavia sono ampiamente bilanciate da una capacità computazionale di gran lunga maggiore che non quella delle reti feed-forward.
Tra le molte caratteristiche delle reti neurali che rivestono interesse, nessuna è probabilmente più suggestiva della loro capacità di apprendere dall'esperienza. Le procedure sviluppate per il loro addestramento sono per molti versi così simili a quelle che la psicologia ha individuato nello sviluppo dell'intelletto umano, che sembra si sia davvero riusciti ad avvicinarsi ad una comprensione fondamentale di questo processo. Non è tuttavia il caso di sopravvalutare questa circostanza, poiché l'apprendimento in una rete neurale è soggetto a limiti di varia natura, e rimangono ancora molti problemi da risolvere prima che si possa definitivamente stabilire se la strada scelta sia quella giusta.
Lo scopo che l'addestramento di una rete neurale persegue è di trovare una distribuzione dei pesi delle connessioni in grado di produrre l'uscita desiderata (o quanto meno, un'uscita coerente) quando venga applicato un dato vettore di ingresso. La procedura di addestramento comincia in generale con la scelta di un insieme di vettori campione di ingresso (il cosiddetto training set) e con l'inizializzazione dei pesi della rete con valori casuali; prosegue poi applicando l'uno dopo l'altro, ripetutamente, i vettori del training set e modificando nel contempo i pesi delle connessioni in base a un algoritmo predeterminato e indipendente dal problema specifico che la rete è chiamata a risolvere. Man mano che il processo si ripete, i pesi convergono verso una distribuzione di valori che produrrà le uscite desiderate.
Gli algoritmi di addestramento vengono classificati in supervisionati e non supervisionati. L'addestramento supervisionato prevede che ciascun vettore del training set venga accoppiato con il corrispondente vettore di uscita desiderato (detto target), in modo che nel complesso essi costituiscano una coppia di addestramento (training pair). Ad ogni applicazione di un vettore di ingresso del training set, l'uscita della rete viene calcolata e confrontata con il target corrispondente; l'errore tra i due vettori di uscita viene quindi utilizzato per stabilire l'entità delle modifiche da apportare ai valori dei pesi delle connessioni all'interno della rete. La procedura viene iterata più e più volte, ogni volta utilizzando tutti i vettori del training set, fino a quando l'errore tra i target e le uscite reali non scende al di sotto di un valore ritenuto accettabile: a questo punto l'addestramento può considerarsi concluso.
Nonostante siano state riportate molte interessanti applicazioni basate sull'addestramento supervisionato, esso è stato da più parti criticato come biologicamente poco plausibile: sembra infatti difficile concepire un meccanismo di addestramento nel cervello in grado di confrontare uscite attuali e uscite desiderate e di propagare poi i relativi errori all'interno delle reti neuronali. Non è chiaro, in tal caso, dove potrebbero essere immagazzinati i target, né quale potrebbe essere la loro origine, né come potrebbe il cervello di un neonato compiere l'auto-organizzazione che è stata ampiamente dimostrata nelle prime fasi dello sviluppo. Allo stato attuale delle conoscenze, l'addestramento non supervisionato sembra dunque un modello molto più plausibile sotto l'aspetto biologico. Sviluppato da T. Kohonen (1984) e da molti altri, esso non richiede alcun vettore target per le uscite, e di conseguenza nessun confronto con uscite idealizzate; il training set corrispondente consiste allora soltanto di vettori di ingresso. L'algoritmo di addestramento modifica i pesi della rete con l'obiettivo di massimizzare la coerenza dei vettori di uscita, di fare cioè in modo che vettori di ingresso simili producano pattern di uscita simili; in altri termini, il processo estrae le proprietà statistiche del training set e costruisce classi di vettori simili. Ovviamente, l'applicazione di un vettore di ingresso appartenente ad una data classe produrrà un ben determinato vettore di uscita, ma non vi sarà alcun modo per stabilire, prima dell'esecuzione della procedura di addestramento, quale valore esso potrà assumere.
Negli anni recenti sono state dimostrate molte interessanti applicazioni delle reti neurali artificiali: nella conversione di testi in rappresentazioni fonetiche (Sejnowski & Rosenberg, 1987), nel riconoscimento di caratteri manoscritti (Burr, 1987), nella compressione di immagini (Cottrell et al., 1987), e così via. Sebbene esse sembrino offrire potenzialità uniche rispetto alle tecniche algoritmiche a tutt'oggi note, sono peraltro affette da un certo numero di limitazioni, alcune piuttosto serie (non ultima, la difficoltà di implementazioni circuitali efficienti, che va però considerato come un problema puramente tecnologico); e in ogni caso esse presentano ancora una gran quantità di aspetti teorici irrisolti. Può darsi che il progredire della conoscenza in campo neurofisiologico si rifletta positivamente nel campo delle reti neurali artificiali, come può benissimo darsi che i progressi teorici nel connessionismo consentano un salto di qualità nella descrizione dei meccanismi nervosi dei sistemi biologici. Probabilmente, l'atteggiamento più sensato da tenere è un cospicuo ottimismo temperato da una buona dose di prudenza: prima che siano perfettamente chiare le implicazioni e le potenzialità di questo approccio, vi è ancora una mole enorme di lavoro da svolgere, e non poche tecniche da sviluppare e da affinare.
(1) Fatte le debite eccezioni per certe
classi di problemi, che richiedono però soltanto intensive manipolazioni di simboli.
(2) Hoff avrebbe in seguito contribuito
all'invenzione del microprocessore.
(3) La prima conferenza open sulle
reti neurali (tutte le precedenti erano state rigorosamente ad inviti) tenuta in questo
periodo fu quella dello IEEE a San Diego, California, nel 1987, ed ebbe un successo
strepitoso, con oltre 1200 partecipanti; gli atti relativi richiesero ben quattro volumi
per la pubblicazione.
(4) Recenti indagini al microscopio
elettronico hanno però mostrato la presenza di numerosi filamenti che congiungono le
membrane pre- e post-sinaptica.
(5) Bullock
(1976) ha elencato ben 46 variabili indipendenti che influiscono sul comportamento del
neurone biologico, delle quali addirittura 23 sono dipendenti dal tempo e almeno 7
dall'attività istantanea.
© 1997-2003 Paolo Marincola (Rome, Italy)
e-mail: pmaNOSPAM@acm.org (eliminare
i caratteri "NOSPAM" per ottenere l'indirizzo esatto)
Commenti, osservazioni e suggerimenti sono estremamente graditi.
Last revised: 2003-11-09 00:30