Reti neurali e riconoscimento di caratteri |
|
In questa sezione intendiamo presentare una breve panoramica delle strutture neurali più usate nella classificazione di caratteri, assieme ad una sommaria discussione dei relativi algoritmi di apprendimento. Va tenuto presente, tuttavia, che il problema più generale della classificazione di pattern può essere affrontato con un numero ben maggiore di architetture neurali che non quelle cui qui si accenna, con risultati che potrebbero senz'altro rivestire un grande interesse. L'argomento è, ovviamente, troppo vasto per essere trattato in questa sede, e in ogni caso non è ancora stato sistematizzato in maniera completa e soddisfacente.
Come abbiamo accennato alla Sez. 7, il primo studio sistematico sulle reti neurali artificiali è apparso in (McCulloch & Pitts, 1943), mentre in (Pitts & McCulloch, 1947) esse sono state per la prima volta sperimentate in un'applicazione legata al riconoscimento di pattern. Le reti studiate da McCulloch e Pitts sono costituite da neuroni in cui il vettore di ingresso x ha componenti binarie, appartenenti cioè all'insieme {0, 1}, e l'attività y è data da:
y = th(w x)
dove th( ) è la funzione di soglia. Successivamente, il neurone di McCulloch-Pitts è stato modificato da Rosenblatt (1958, 1959, 1961) in maniera che le componenti del vettore di ingresso e del vettore dei pesi potessero assumere valori continui; un'ulteriore variante, impiegata in applicazioni di controllo adattativo, è dovuta a Widrow et al. (Widrow & Hoff, 1960; Widrow, 1961; Widrow & Angell, 1962; Widrow, 1963).
Le reti utilizzate da Rosenblatt sono note col nome di perceptron, e, sebbene esse siano costituite da un solo strato di neuroni, tale denominazione è stata applicata anche a reti costituite da più strati, come quelle precedentemente illustrate in Fig. 23. La sostanziale innovazione dovuta a Rosenblatt consiste però nella scoperta di un algoritmo di training supervisionato per il perceptron a un solo strato, la cosiddetta delta rule. Sia x un vettore del training set e W la matrice dei pesi della rete; sia ancora y il vettore delle attività dei neuroni conseguente all'applicazione di x, dato da y = th(W x), e y' il vettore di attività desiderato (target). Allora l'errore tra il vettore target e il vettore delle attività è dato da:
d = y' – y
e la delta rule stabilisce che la matrice dei pesi vada modificata in una nuova matrice W' tale che:
W' = W + edxT
La scoperta della delta rule permise dunque negli anni '60 di portare le reti neurali dal campo puramente speculativo alle applicazioni pratiche, principalmente a quelle legate alla classificazione di pattern; i successi conseguiti in questa categoria di problemi, che sono notoriamente complessi sotto l'aspetto algoritmico e che sembrano richiedere un comportamento "intelligente" ad una macchina che pretenda di affrontarli, contribuirono senza dubbio al grande entusiasmo che in quegli anni circondava le reti neurali. Il lavoro critico di Minsky e Papert (Minsky, 1969), che pose fine a questi eccessivi ottimismi, dimostrò essenzialmente come la delta rule sia capace di addestrare un perceptron classificatore soltanto se le categorie sono linearmente separabili (Fig. 24). Ma anche se nello stesso lavoro veniva dimostrato come categorie non linearmente separabili possano essere classificate con un perceptron a più strati, e che un perceptron a tre strati (Fig. 25) ha le stesse capacità computazionali di uno con un numero di strati arbitrariamente maggiore di 3, tuttavia la mancanza di algoritmi di training per queste reti multilayer rese vano ogni ulteriore tentativo di applicazione: se la delta rule era in grado di aggiornare i pesi delle connessioni afferenti ai neuroni dello strato di uscita, non era per nulla chiaro in che modo essa consentisse di modificare anche quelli delle connessioni afferenti ai neuroni degli strati intermedi (detti anche nascosti perché inaccessibili sia dal lato degli ingressi che da quello delle uscite).
|
|
La scoperta dell'algoritmo di training per il perceptron multistrato è stata piuttosto movimentata, come abbiamo accennato nella Sez. 7, e solo dopo il lavoro di Rumelhart et al. (1986) tale tecnica conosce una vasta diffusione nella comunità scientifica col nome di back-propagation. L'unica variante che l'algoritmo richiede al neurone di Rosenblatt è che la funzione di attivazione sia differenziabile, sicché nella maggior parte delle applicazioni la scelta cade sulla funzione sigmoide s(u) per via della semplicità della sua derivata:
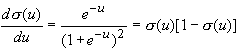
La back-propagation, che è in fondo una variante piuttosto ingegnosa della delta rule, è ancor oggi molto popolare, e le applicazioni che utilizzano perceptron multistrato sono senza dubbio la grande maggioranza di quelle riportate dalla letteratura. Tuttavia, la back-propagation soffre di un certo numero di inconvenienti, tra cui è qui il caso di citare solo i più evidenti.
Il primo problema, costituito dalla lentezza della convergenza dei valori dei pesi, che impone un gran numero di iterazioni alla procedura di training, è stato affrontato da molti ricercatori, e sembra qui opportuno citare solo due tra le varie modifiche all'algoritmo originale che sono state proposte negli ultimi anni. Parker (1987) descrive un metodo per aumentare la velocità di convergenza, chiamato back-propagation del secondo ordine, dove viene usata anche la derivata seconda della funzione di attivazione, e dimostra come l'algoritmo sia ottimale, nel senso che l'uso di derivate di ordine superiore non comporta ulteriori miglioramenti; non è ancora del tutto chiaro se i requisiti computazionali di tale metodo, significativamente maggiori che non nella back-propagation standard, siano giustificati dalla maggior velocità di convergenza che se ne può ottenere. Tuttavia, introducendo minimi cambiamenti nel campo di variabilità degli ingressi e delle uscite dai neuroni nascosti, è possibile (Stornetta & Huberman, 1987) diminuire il tempo di convergenza dell'algoritmo standard per un fattore che va dal 30% al 50%.
Il secondo problema, quasi sempre risolto in maniera empirica nelle applicazioni, è dovuto all'assenza di criteri sicuri in base a cui determinare il numero ottimale di neuroni degli strati nascosti; la questione viene dibattuta in molti lavori (Kung & Hwang, 1988; Baum, 1988; Mirchandani & Cao, 1989), il più recente dei quali (Huang & Huang, 1991) fornisce risultati interessanti soprattutto nel caso in cui la rete debba realizzare funzioni binarie. Questa circostanza si verifica abbastanza spesso nel riconoscimento di caratteri, quando il pattern venga applicato direttamente all'ingresso della rete o quando il vettore delle feature è di tipo binario e ciascuna componente rappresenta la presenza o l'assenza della feature corrispondente.
Un ulteriore inconveniente dell'algoritmo di back-propagation, che su una immaginaria superficie nello spazio multidimensionale degli errori fa muovere la rete verso regioni di minimo, è dovuto al fatto che tale superficie è in generale costellata di minimi locali, entro i quali la rete può restare intrappolata nel corso della ricerca di un minimo globale. Sono stati proposti diversi metodi statistici per superare questa difficoltà, ma essi in genere rallentano ulteriormente l'algoritmo di training. Wassermann (1988) propone una combinazione della back-propagation con metodi statistici che sembra in grado di raggiungere i minimi globali nella superficie degli errori senza tuttavia diminuire apprezzabilmente la velocità di convergenza.
Il lavoro di Hopfield (1982, 1984) ha fatto praticamente rinascere l'interesse per le reti neurali come strumenti computazionali. Le reti di Hopfield hanno un solo strato di neuroni e sono del tipo ricorrente, dove ogni neurone è connesso con tutti gli altri. Nel neurone di Hopfield, gli ingressi possono assumere valori nell'insieme {–1, +1}, i pesi possono assumere qualunque valore e la funzione di attivazione è ancora la funzione di soglia th(u) con valori nell'insieme {–1, +1}. Ad ogni rete ricorrente è associata una dinamica della struttura, costituita dalla sequenza di stati assunti dalla rete stessa; nella rete di Hopfield, lo stato è semplicemente un vettore che coincide col vettore delle attività y dei neuroni. Il vettore di ingresso x ha allora lo stesso numero di componenti di y, e viene applicato alla rete forzando ciascun neurone ad assumere come uscita il valore della corrispondente componente dell'ingresso; in altri termini, la rete viene inizializzata ponendo y = x. A questo punto, la rete viene lasciata libera di evolversi ricalcolando continuamente i nuovi valori di attività in funzione di quelli correnti; detto yn lo stato della rete all'istante tn, lo stato successivo viene calcolato come
yn+1 = W yn
dove il generico elemento wij della matrice W è il peso della connessione che porta l'uscita del j-esimo neurone all'ingresso dell'i-esimo neurone. Accanto a questo tipo di funzionamento, detto sincrono perché tutte le attività vengono aggiornate nello stesso istante, ve ne è anche uno asincrono, in cui di volta in volta viene aggiornata l'uscita di un solo neurone scelto a caso.
Nelle reti ricorrenti vi è naturalmente un problema di stabilità, nel senso che non è detto a priori che la rete riesca a convergere su uno stato stabile. Hopfield ha introdotto una funzione chiamata energia della rete (analoga per molti versi alle funzioni di Lyapunov nei sistemi dinamici):
![]()
e ha dimostrato che, in regime di funzionamento asincrono, se W è simmetrica e gli elementi della sua diagonale principale sono nulli, se cioè wij = wji e wii = 0, allora il valore di E non può aumentare nel passaggio da uno stato all'altro; poiché E non può evidentemente raggiungere valori infinitamente negativi, ne consegue che prima o poi lo stato della rete cesserà di cambiare, ed essa raggiungerà dunque con certezza uno stato stabile.1
L'addestramento della rete di Hopfield è di tipo non supervisionato e richiede una sola iterazione sul training set. Siano x1, x2, ..., xk i vettori del training set; allora la matrice W è data da
W = x1 x1T + x2 x2T + ... + xk xkT
Contrariamente al perceptron, la rete di Hopfield non viene utilizzata come classificatore, ma come memoria associativa: una volta applicato in ingresso un pattern x, la rete si stabilizzerà su una configurazione corrispondente a quello tra i pattern del training set più "simile" ad x. Sono state dimostrate applicazioni in cui una rete di Hopfield riesce a riconoscere un pattern nonostante la presenza di distorsioni o di rumore, oppure a ricostruire un pattern a partire da una sua porzione (Lippmann, 1987). Le reti di Hopfield sono poi state generalizzate (Hopfield, 1984) al caso in cui la funzione di attivazione è una sigmoide modificata:
![]()
dove l è un coefficiente che determina la forma della funzione di attivazione: quando più l è grande, tanto più la sigmoide si approssima ad una funzione di soglia con valori nell'intervallo [0, 1].
Oltre che come memorie associative, le reti di Hopfield sono state utilizzate per la soluzione di problemi di ottimizzazione (Hopfield & Tank, 1985; Tank & Hopfield, 1986), come quello del commesso viaggiatore (Traveling Salesman Problem), che può brevemente essere descritto come segue: dato un insieme di città da visitare e le loro distanze relative, si debba trovare il percorso più breve che consenta di visitarle tutte attraversandole una e una sola volta, ritornando infine al punto di partenza. E' stato dimostrato come questo problema sia NP-completo (Garey & Johnson, 1979), il che equivale a dire che non è noto a tutt'oggi alcun metodo generale migliore di quello per prova ed errore.2 Poiché la ricerca esaustiva della soluzione ottima è del tutto impraticabile quando il numero delle città comincia a crescere, è pratica comune ricorrere a metodi empirici od euristici per trovare una soluzione sub-ottimale. La soluzione proposta in (Hopfield & Tank, 1985) è esemplare al riguardo: la rete neurale non garantisce una soluzione ottima, ma quella che riesce a trovare viene fornita in tempi talmente brevi da risultare utile in moltissimi casi.
Purtroppo, neanche le reti di Hopfield possono dirsi prive di inconvenienti. Di questi, il principale è costituito dalle limitazioni cui soggiace il numero di pattern memorizzabili nella rete. In primo luogo, poiché l'attività di ogni neurone può assumere solo due valori, è chiaro che una rete da N neuroni può assumere solo 2N stati distinti: è questo dunque il limite massimo teorico al numero di pattern memorizzabili. Inoltre, è naturale che, per essere discriminati, due pattern del training set devono essere sufficientemente diversi l'uno dall'altro; tale condizione può essere espressa in termini di ortogonalità dei vettori corrispondenti, e lo stesso Hopfield (1982) ha quantificato sperimentalmente in circa 0.15N il numero di pattern che la rete è generalmente in grado di memorizzare in maniera corretta. Quando il numero di pattern memorizzati supera determinati limiti, la rete può non riuscire a stabilizzarsi su alcuno di essi, oppure converge su un pattern diverso da tutti quelli con cui è stata addestrata. Sebbene vi siano in letteratura convincimenti contrastanti in proposito, sembra abbastanza affidabile e confermato dagli esperimenti il risultato (Abu-Mostafa & St. Jacques, 1985) secondo cui il numero di pattern memorizzabili non può superare N.
In determinate condizioni, la rete di Hopfield tende a stabilizzarsi su minimi locali della funzione di energia anziché su un minimo globale. Questo problema viene risolto ricorrendo a una classe di reti note come macchine di Boltzmann, in cui i neuroni cambiano di stato in maniera statistica anziché deterministica. Viene sfruttata la stretta analogia tra questi metodi e il modo in cui un metallo viene raffreddato in certi processi metallurgici; di conseguenza, i metodi relativi (Kirkpatrick et al., 1983) vengono detti raffreddamenti simulati (simulated annealing).
Un metallo viene temperato riscaldandolo ad una temperatura superiore al suo punto di fusione, e quindi lasciandolo raffreddare lentamente. Ad alte temperature, gli atomi possiedono energie elevate e si muovono liberamente e casualmente assumendo ogni possibile configurazione. Via via che la temperatura viene gradualmente abbassata, le energie atomiche diminuiscono e il sistema nel suo complesso tende ad assestarsi in una configurazione di minima energia. Alla fine, quando il raffreddamento è completo, si raggiunge uno stato dove l'energia del sistema è a un minimo globale.
Ad una data temperatura T, la distribuzione di probabilità delle energie del sistema è determinata dal fattore di probabilità di Boltzmann e-E/kT, dove E è l'energia del sistema e k è la costante di Boltzmann; vi è dunque una probabilità finita che il sistema possegga alte energie anche a temperature basse. La distribuzione statistica delle energie consente tuttavia al sistema di "saltare" fuori da un minimo locale di energia; allo stesso tempo, la probabilità di energie elevate nel sistema decresce rapidamente al diminuire della temperatura. Ne consegue che, a basse temperature, si hanno ottime probabilità che il sistema venga a trovarsi in uno stato di bassa energia.
Se le regole per la transizione di stato in una rete binaria di Hopfield vengono determinate statisticamente anziché in modo deterministico, ne risulta un sistema con raffreddamento simulato. A questo fine, viene determinata la probabilità p di un cambiamento di stato Dy:
![]()
dove T è una temperatura artificiale.
Nella fase iniziale dell'algoritmo, la temperatura artificiale T parte da un valore elevato, i neuroni vengono forzati in uno stato iniziale determinato dal vettore di ingresso, e la rete viene messa in condizioni di cercare un minimo di energia secondo la procedura che segue:
Questa tecnica, descritta nei dettagli da Hinton e Sejnowski (1986), richiede di solito tempi di addestramento lunghissimi, ma può essere estesa a reti con virtualmente qualunque configurazione, benché non sia sempre possibile garantirne la stabilità.
Un principio che appare fondamentale nella struttura delle vie percettive del cervello consiste nel particolare ordine della disposizione dei neuroni, che spesso riflette determinate caratteristiche fisiche dello stimolo esterno ricevuto (Kandel & Schwartz, 1985). Ad esempio, nei vari livelli delle vie uditive sia le cellule che le fibre nervose hanno una disposizione anatomica legata alla frequenza di massima sensibilità di ciascun neurone, e una simile organizzazione tonotopica si estende fino alla corteccia uditiva (Moller, 1983; Kandel & Schwartz, 1985). Benché una gran parte di queste organizzazioni, soprattutto ai livelli più bassi, sia geneticamente predeterminata, sembra verosimile supporre che ai livelli superiori esse vengano create spontaneamente mediante processi di apprendimento per esperienza. Kohonen (1984) discute un processo del genere, rivolto a produrre quelle che egli chiama mappe auto-organizzanti di feature (self-organizing feature maps), e che presentano forti rassomiglianze con quelle scoperte nel cervello.
La rete di Kohonen è costituita da N ingressi a valori continui e da un solo strato bidimensionale di M neuroni, con connessioni tra ciascun ingresso e ciascun neurone; la matrice W dei pesi viene inizializzata con valori piccoli ma casuali. Nell'algoritmo di addestramento non supervisionato proposto da Kohonen, i vettori del training set vengono ripetutamente presentati all'ingresso della rete; per ogni vettore x applicato, vengono modificati solo i pesi delle connessioni afferenti a quei neuroni che giacciono in un dato intorno del neurone che fornisce la massima risposta ad x; inoltre, al progredire delle iterazioni di addestramento, il raggio dell'intorno in questione viene via via diminuito. Ad addestramento concluso, la rete di Kohonen produce un quantizzatore vettoriale (Gray, 1984), in cui i vettori dei pesi delle connessioni afferenti ai vari neuroni specificano delle categorie e campionano lo spazio N-dimensionale di ingresso in modo tale che la loro densità tende ad approssimare la densità di probabilità dei vettori di ingresso (Kohonen, 1984). Per di più, i pesi risulteranno organizzati in maniera che ingressi fisicamente simili producano la massima risposta in neuroni topologicamente vicini, inducendo così un ordinamento naturale nello strato di neuroni.
Oltre alle giustificazioni teoriche del comportamento della rete, Kohonen (1984) discute anche un gran numero di esempi; in letteratura si trovano poi molte altre applicazioni interessanti, di cui citiamo qui soltanto un quantizzatore vettoriale utilizzabile nei riconoscitori vocali (Kohonen et al., 1984) e una struttura per l'organizzazione delle relazioni semantiche tra parole (Ritter & Kohonen, 1989).
(1) E' stato dimostrato (Cohen & Grossberg, 1983) che ogni rete ricorrente avente
matrice dei pesi simmetrica e diagonale principale nulla è stabile.
(2) Alcuni matematici congetturano
addirittura che per problemi NP-completi non sia possibile trovare metodi migliori.
© 1997-2003 Paolo Marincola (Rome, Italy)
e-mail: pmaNOSPAM@acm.org (eliminare
i caratteri "NOSPAM" per ottenere l'indirizzo esatto)
Commenti, osservazioni e suggerimenti sono estremamente graditi.
Last revised: 2003-11-09 00:30