(1) M. Mano, C.R. Kime, "Logic and Computer Design Fundamentals, Third Edition", Prentice Hall, 2003, ISBN 013140539X.
http://www.amazon.com/exec/obidos/ASIN/013140539X

(2) R.H. Katz, G. Borriello, "Contemporary Logic Design (2nd Edition)", Prentice Hall, 2004, ISBN 0201308576.
http://www.amazon.com/exec/obidos/ASIN/0201308576

(3) J.F. Wakerly, "Digital Design: Principles and Practices (4th Edition)", Prentice Hall, 2005, ISBN 0131863894.
http://www.amazon.com/exec/obidos/ASIN/0131863894

Mi faccia sapere se le servono altre informazioni.

Vorrei chiederle se posso prendere come riferimento di prova di esame quelle del corso di calcolatori 2.

Si', ma non esattamente come riferimento. Il progetto di Reti Logiche sara' necessariamente un tantino piu' complesso che non uno di Calcolatori 2.

Ho visto l'appello che ha dato per gli studenti del vecchio ordinamento, ma anche la parte di interfaccia al PD32 la dobbiamo svolgere anche noi studenti del nuovo ordinamento?

Anche se in teoria, trattandosi di argomenti che avete svolto in corsi precedenti, sareste tenuti a conoscerli e a utilizzarli, diciamo pure che per il N.O. non ci sara' interfacciamento al PD32 -- o quanto meno non ci sara' software da scrivere. Tuttavia, potrebbe accadere (come del resto accade nella realta') che il vostro progetto debba in qualche modo "comunicare" con un'entita' esterna, e allora il problema dell'interfacciamento si presentera' di nuovo, anche se sotto forma diversa.

Nella lezione di oggi, nella realizzazione di un FF JK a partire da un > FF SR, si era trovato:

S=NAND(J,Q*)
R=NAND(K,Q)

No, se ben ricorda, dalle mappe di Karnaugh avevamo ottenuto

S = J Q* = AND(J,Q*) ; S=1 se J=1 e Q=0, in maniera da forzare Q=1
R = K Q = AND(K,Q) ; R=1 se K=1 e Q=1, in maniera da forzare Q=0

Dunque AND(), non NAND().

Poi siccome S e R entravano in NAND con il clock, abbiamo trasformato il nand di nand in una singola porta nand a tre ingressi, per esempio:

NAND(NAND(J,Q*),ck*) -> NAND(J,Q*,ck*)
NAND(NAND(K,Q),ck*) -> NAND(K,Q,ck*)

Ma le due espressioni non sono diverse? (trasformandole con de morgan il nand di nand viene: JQ*+ck e il nand a tre ingressi viene: J*+Q+ck).

Le espressioni non sono di conseguenza queste, ma:

NAND(AND(J,Q*),ck*) = NAND(J,Q*,ck*)
NAND(AND(K,Q),ck*) = NAND(K,Q,ck*)

Tutto chiaro adesso?

(1) se il counter e' programmato in "up", un dato bit commuta quando tutti i bit meno significativi rispetto ad esso sono ad "1" (Q0, in particolare, commuta sempre)

(2) se il counter e' programmato in "down", un dato bit commuta quando tutti i bit meno significativi rispetto ad esso sono a "0" (Q0, in particolare, commuta sempre)

Ed e' facile vedere che le equazioni riportate negli appunti codificano proprio questa legge! 

Avrei 2 domande da porle.
La prima riguarda il programma:
- Occorre studiare anche la parte relativa alle reti LLC SCA, SCO? PD32?

Per quanto riguarda LLC SCA e SCO, la risposta e' si'; tuttavia, va chiarito che di tutto l'argomento va studiata solo la parte che puo' in qualche modo essere coinvolta nei progetti, senza tutti gli approfondimenti teorici che si trovano sul libro di testo.

Per quanto riguarda il PD-32, poiche' abbiamo stabilito che nei progetti d'esame non ci sara' software da scrivere (almeno per gli studenti del Nuovo Ordinamento), gli unici argomenti da rinfrescare -- cosa che sto facendo a lezione -- sono: cicli di Input/Output sul bus PD-32, implementazione di porte di Input/Output sull'interfaccia, generazione di interrupt e ciclo di Interrupt Acknowledge. In pratica, quasi tutto cio' che ha a che fare con il trasferimento di dati tra CPU e interfaccia.

La seconda riguarda le esercitazioni:
- fanno parte degli appunti del Prof. Chiari in vendita presso ingegneria 2000, in caso di risposta negativo le chiedo dove è possibile reperire tali esercitazioni

Molte esercitazioni sono riprese dagli appunti che lei cita (tutt'al piu' con qualche variante di poco conto); dei (pochi) argomenti trattati a lezione che non sono compresi ne' nei testi di Cioffi ne' negli appunti di Chiari, lei trovera' comunque dei riferimenti sul sito su cui studiare. Per quanto riguarda invece gli esempi di progetti svolti a lezione, purtroppo non ci sono documenti scritti (ma qualcosa sto preparando); in ogni caso, puo' sempre fare riferimento ai numerosi progetti d'esame corredati di soluzione che sono gia' presenti sul sito come riferimento.

Oggi (21/11) durante lo sviluppo del progetto mi sono perso qualche passo iniziale nell'interfacciamento della periferica (Dev) al bus dati.I dati ricevuti da Dev sono essenzialmente i bit seriali di un canale esterno sincronizzati ad un clock(e il clock stesso), e il dato T di confronto per generare l'interrupt, proveniente dalla cpu.

Andiamo con ordine. La periferica riceve:

(1) dal mondo esterno: un canale bit-seriale (XDAT) con relativo clock di sincronismo (XCLK)

(2) dalla CPU: una maschera M a 32 bit (con cui confrontare *ogni* sottostringa da 32 bit che appare sul canale seriale), e un valore di soglia T a 6 bit (con cui confrontare il valore generato dal confronto precedente)

Per quale motivo abbiamo trattato i due eventi di ricezione dati come se fossero due cicli di Output della cpu?

Perche' dalla CPU, come abbiamo detto, riceviamo due dati: la maschera di riferimento e il valore di soglia.

Come possiamo gestire il fatto che i dati siano seriali? Potremmo utilizzare il dato(il singolo bit) direttamente per caricare uno shift register in configurazione sipo

E' esattamente cio' che abbiamo fatto.

le cui uscite seriali sono abilitate da un TC di un contatore mod 3, e avere poi la catena di CC come visto?

Perche' mai un contatore mod 3? La sequenza di operazioni

(a) accumulo degli ultimi 32 bit arrivati su XDAT (realizzato, come lei giustamente osserva) con uno shift register in confgurazione SIPO)

(b) confronto di questi con la maschera M, realizzato con un array di XNOR

(c) determinazione del numero di bit uguali tra sottostringa e maschera (realizzato con l'addizionatore speciale di cui si parlava a lezione)

(d) confronto di (c) con la soglia T (realizzato con un normale comparatore binario a 6 bit)

questa sequenza deve essere eseguita PER OGNI NUOVO DATO XDAT in arrivo, dunque deve essere replicata ad *ogni* XCLK, dal momento che la sottostringa a 32 bit viene aggiornata ed alterata ad ogni XCLK; di conseguenza, non c'e' nulla da contare (poiche' le varie operazioni sulla singola sottostringa possono essere tranquillamente eseguite in parallelo) e non c'e' da tener memoria di nulla tra un XCLK e l'altro, poiche' le operazioni su una data sottostringa non sono influenzate da alcuna operazione su alcun'altra sottostringa.

Questo circuito, tuttavia, e' piuttosto speciale, poiche', pur avendo un loop combinatorio -- il che porterebbe a pensare che si tratta di un circuito asincrono, dunque dotato di memoria -- in realta' continua a comportarsi come circuito combinatorio, ossia dove le uscite sono funzione solo degli ingressi attuali e non della loro storia, come vedremo tra breve.

Come si fa ad analizzarlo? Ci sono due vie, l'una analitica (scriviamo le equazioni che regolano i livelli logici sui vari nodi, e ricaviamo le funzioni ingresso-uscita) e l'altra, piu' semplice ed immediata, che consiste nel costruire la tavola di verita' e da questa ricavare le funzioni ingresso-uscita.

Intanto cominciamo ad osservare che il circuito e' perfettamente simmetrico, il che significa che se io riesco a ricavare ad esempio la funzione y1 = f (x1, x2, x3) posso poi ottenere direttamente le altre due semplicemente ruotando le variabili:

y2 = f (x2, x3, x1)
y3 = f (x3, x1, x2)

Questo significa allora che non e' necessario valutare tutte e otto le possibili combinazioni di ingresso, ma e' sufficiente studiare che cosa accade con le seguenti combinazioni:

(x1 x2 x3) = (0 0 0), (1 0 0), (1 1 0), (1 1 1)

tutti gli altri risultati li ottengo per simmetria ruotando sia le variabili di ingresso che quelle di uscita.

Adesso segua l'analisi sulla figura che le mando in allegato, dove ho dato dei nomi ai nodi interni del circuito e alle singole porte, per facilitarne il riferimento. Nel seguito, indichero' con x* la negazione di x.

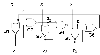
kautz.gif

Primo caso (x1 x2 x3 = 0 0 0) - Per le proprieta' dell'operatore NOR, G1 G3 e G5 si comportano da invertitori rispetto a z1 z2 z3, ossia avremo y1 = z1*, y2 = z2*, y3 = z3*. Di conseguenza, ciascuna delle porte G2 G4 G5 vedra' ai propri ingressi due livelli complementari, e quindi per le proprieta' del NOR tutte e tre non potranno che avere uscita 0. Dunque, essendo z1 = z2 = z3 = 0, avremo anche y1 = y2 = y3 = 1.

Secondo caso (x1 x2 x3 = 1 0 0) - Intanto sara' sicuramente y1 = 0. Le porte G3 G5 si comportano da invertitori rispetto a z2 z3; G4 e G6 vedono ai propri ingressi due livelli complementari; e dunque sara' z3 = z1 = 0; e quindi z2 = 1. In definitiva, avremo y1 = 0, y2 = 0, y3 = 1.

Terzo caso (x1 x2 x3 = 1 1 0) - Intanto sara' sicuramente y1 = y2 = 0. La porta G5 si comporta da invertitore rispetto a z3; G6 vede ai propri ingressi due livelli complementari e dunque sara' sicuramente z1 = 0. Pertanto avremo z2 = 1, z3 = 0; con conseguente y3 = 1.

Quarto e ultimo caso (x1 x2 x3 = 1 1 1), il piu' interessante. Le uscite saranno senz'altro y1 = y2 = y3 = 0. Tuttavia, avremo anche z2 = z1* = z3 = z2*, che NON e' una contraddizione! Significa semplicemente che il loop combinatorio che comprende i nodi z1 z2 z3 entra in oscillazione; ma e' anche vero che questa oscillazione, ossia questa variazione continua di z1 z2 z3 *NON* influenza minimamente le uscite y1 y2 y3, che continuano a restare tranquillamente fisse a zero!

A questo punto, sfruttando le simmetrie di cui dicevamo prima, possiamo costruire la nostra tavola di verita':

x1 x2 x3 y1 y2 y3
--------------------
0 0 0 1 1 1
0 0 1 0 1 0
0 1 0 1 0 0
0 1 1 1 0 0
1 0 0 0 0 1
1 0 1 0 1 0
1 1 0 0 0 1
1 1 1 0 0 0

Adesso basta costruire un mappa di Karnaugh ad esempio per la sola y1, ed otterremo

y1 = x1* x2 + x1* x3* = x1* (x2 + x3*)

Le altre due funzioni sono ottenute da questa per rotazione delle variabili, o da analoga analisi sulla tavola di verita':

y2 = x2* (x3 + x1*)
y3 = x3* (x1 + x2*)

Questa categoria di circuiti e' stata scoperta nel 1970, con lo scopo di dimostrare che in determinate circostanze e' *necessario* introdurre loop combinatori per realizzare un sistema di funzioni combinatorie col *minimo* numero possibile di porte. Ovviamente, circuiti di questo genere hanno solo interesse accademico ma non vengono mai utilizzati in pratica, poiche' l'oscillazione che ha luogo quando gli ingressi sono tutti a 1 assorbe una gran quantita' di energia dall'alimentazione.

Volevo chiedere conferma del fatto che l'esercizio di oggi non avesse bisogno di uno SCO in quanto tutti i segnali di controllo (il CE del contatore e gli OE in uscita) venivano generati internamente dallo SCA.

Si', e' cosi'. In realta', e' il contatore di indirizzi di ROM che funge da SCO -- ogni qual volta c'e' una sequenza di operazioni che si sviluppa lungo piu' di un periodo di clock, e della quale e' possibile identificare una fase di inizio e una fase di completamento, ogni volta c'e' necessariamente uno SCO, realizzato in maniera esplicita o, come in questo caso, implicita.

Poi volevo chiedere come mai abbiamo fatto una scansione lineare della ROM invece che logaritmica.

Per una serie di ragioni, che ho anche elencato a lezione:

(1) la versione con ricerca logaritmica avrebbe richiesto un tempo maggiore per l'esposizione del progetto, e questo tempo stamattina non ce l'avevamo;

(2) trattandosi di un progetto assegnato a Calcolatori 2 (secondo anno) sarebbe stato eccessivo esigere che gli studenti sapessero maneggiare un algoritmo di ricerca logaritmica (ma ce n'e' stato uno che me l'ha fatta e, se non ricordo male, ha di conseguenza beccato un 30 e forse anche la lode);

(3) poiche' l'architettura del progetto cambia solo in piccola parte nel passaggio da ricerca lineare a ricerca logaritmica, e poiche' da studenti del quarto anno *e' lecito* aspettarsi che conoscano bene la ricerca logaritmica, l'estensione a quest'ultima potrebbe essere un buon tema per uno dei prossimi appelli :-)

Se ne ha voglia e/o tempo e/o possibilita', provi a sviluppare da solo la modifica, e magari venga poi a farmela vedere.

(1) La ROM ha 2^20 parole, dunque l'indirizzo deve essere da 20 bit e non da 5 come nel suo progetto -- occorre estendere l'architettura a 20 flip-flop anziche' soltanto a 5.

(2) E' preferibile mai usare flip-flop SR, che in genere possono dare problemi; nel suo caso, potrebbe tranquillamente utilizzare ad esempio flip-flop JK sincronizzandoli al clock.

(3) Il circuito di Start mi sembra inutilmente complicato: la scrittura di VAL puo' semplicemente generare il Clear per il contatore, dopo di che il tutto puo' girare tranquillamente da solo, asservito solo alle uscite dal comparatore come lei ha fatto.

(4) Se lei ha l'accortezza di bloccare il contatore e di disabilitare il decoder in presenza delle condizioni di terminazione, il registro in uscita dalla ROM non ha piu' ragione di esistere.

(5) La lettura del risultato deve essere abilitata non da IACK ma da una combinazione IORD*SEL.

(6) Il flip-flop che genera Interrupt Request puo' essere semplicemente un JK con J = END e K = 0, eliminando cosi' l'OR di controreazione tra Q e D.

(Quello che lei ha usato, per inciso, e' esattamente l'algoritmo impiegato nei cosiddetti "convertitori analogico/digitali ad
approssimazioni successive", in cui la tensione incognita di ingresso viene confrontata con una serie di tensioni di riferimento ordinate in maniera crescente, e ad ogni clock viene generato un nuovo bit del campione in uscita.)

(Una possibile diversa architettura avrebbe potuto essere quella che prevede due registri puntatori RMIN e RMAX inizializzati col minimo e il massimo indirizzo di ROM, il puntamento alla ROM con la media M tra i due, e la sostituzione dell'uno o dell'altro con M in caso di ricerca fallita; andrebbe tuttavia in tal caso studiata accuratamente la condizione di terminazione qualora la chiave cercata non esistesse in ROM.)

Comunque complimenti: come ho detto, ha impostato un buon lavoro.